International Symposium on the Latest Development of Biomathematics Modeling, Analysis, and Applications

Schedule

(Time Zone: Beijing Time)

Abstracts

Case Importations During the COVID-19 Pandemic

Julien Arino, University of Manitoba, julien.arino@umanitoba.ca

Abstract

COVID-19 spread worldwide in an unprecedented manner, reaching most places in a matter of months. Looking into the details, though, it is apparent that spread was not homogeneous and that considering spread to local jurisdictions instead of national or territorial ones, one paints a very different picture, with some locations experiencing long, widespread propagation and others seeing sporadic outbreaks followed by periods where the disease was absent. The situation is even more nuanced when one considers the different variants of SARS-CoV-2 that have emerged since the start of the pandemic. For jurisdictions experiencing on and off propagation, one of the main issues is that of case importations. Most places are subject to "stimuli" where individuals infected in other locations travel to the location of concern while bearing the disease. I will present work that has been ongoing since the beginning of the pandemic that considers the reaction of places to such stimuli through two main questions: 1) what determines the probability that an imported case leads to a local outbreak and what is the efficacy of control measures against this and 2) what is the contribution of imported cases to an outbreak at different stages during that outbreak?

Delayed Regulation in Physiology and Epidemiology

Jacques Bélair, Université de Montréal, jacques.belair@umontreal.ca

Abstract

The description of the regulation of many biological processes involves the incorporation of explicit time delays to account for such elements as the latency period in infection, or the maturation interval in proliferating cell production. By developing biologically correct models of these systems, we are naturally lead to the investigation of nonlinear systems of delay-differential equations, some with state-dependent delays, which we can investigate to establish dynamical properties (stability, bifurcations) of the underlying systems. I will present two classes of examples where such analysis has been performed: interacting populations in which a virus is circulating, and models for instabilities in erythropoiesis (red blood cell production) and thrombopoiesis (platelet production).

Mathematical Modelling of the Transmission Dynamics of Opisthrochiasis

Nakul Chitnis, Swiss Tropical and Public Health Institute, Nakul.Chitnis@unibas.ch,

Abstract

The trematode liver fluke (flat worm), Opisthorchis viverrini, is prevalent is southeast Asia, causing the chronic hepatobiliary disease, opisthorchiasis. Long term infection can lead to the bile duct cancer, cholangiocarcinoma, which is typically fatal. We develop an ordinary differential equation (ODE) model of the transmission dynamics of O. viverrini through its life cycle in snails, fish, and humans and reservoir hosts such as domestic cats and dogs; and a second partial differential equation (PDE) model that includes heterogeneity in age in humans. We calibrate these models to data collected from two communities in Khong Island in Southern Lao PDR, using maximum likelihood estimates and Bayesian sampling-resampling methods. We define basic reproduction numbers and type-reproduction numbers for these models to show that humans can maintain the transmission cycle through snails and fish, so interventions targeting humans with a sufficiently high coverage could eliminate transmission. Numerical simulations suggest that, as compared to improved sanitation and behaviour change campaigns, treating humans at least once a year increases the probability of achieving elimination and reduces the time to elimination. We finally develop a stochastic individual-based model that better captures heterogeneity in the intensity of infection in the human population and the impact of intervention campaigns on high intensity infections in humans.

异质性传染病动力学模型与应用

Jingan Cui, Beijing University of Civil Engineering and Architecture, cuijingan@bucea.edu.cn

Abstract

传染病的传播与控制过程中，基本再生数、最终规模、免疫策略问题的研究至关重要。针对异质的多群组传染病模型探讨了基本再生数与最终规模的关系，应用于一些传染病案例与免疫策略的研究。

Stability and Bifurcation of a Reaction-Diffusion-Advection Model with Nonlinear Boundary Condition

Binxiang Dai, Central South University, bxdai@ecsu.edu.cn

In this talk, we consider a reaction-diffusion-advection population model with nonlinear boundary condition. Firstly, the stability of the trivial steady state is investigated by studying the corresponding eigenvalue problem. Secondly, the existence and stability of nontrivial steady states are proved by applying the Crandall-Rabinowitz bifurcation Theorem, the Lyapunov-Schmidt reduction method and perturbation method, in which bifurcation from simple eigenvalue and that from degenerate simple eigenvalue are both possible. The general results are applied to a parabolic equation with monostable nonlinear boundary condition, and to a parabolic equation with sublinear growth and superlinear boundary condition.

Global Threshold Dynamics of SIQS Model in Time Fluctuating Environment

Meng Fan, Northeast Normal University, mfan@nenu.edu.cn

Abstract

The global threshold dynamics of an SIQS model in fluctuating environments are explored. Criteria are established for the permanence and extinction of the infective in general nonautonomous scenario. In particular, an environment varying periodically in time is further considered. The global threshold dynamics (i.e., the existence and global asymptotic stability of the disease-free periodic solution, the existence of the endemic periodic solution and the permanence of the infective) are completely characterized by the basic reproduction number defined by the spectral radius of an associated linear integral operator.

Forced Waves of the Fisher-KPP Equation in Time-Periodic Shifting Environment

Jian Fang, Harbin Institute of Technology, jfang@hit.edu.cn

Abstract

In this talk we first discuss the existence, uniqueness and attractivity of the forced wave for the Fisher-KPP equation in time-periodic shifting environment, and then we apply the result to an SIS epidemic model.

Modelling COVID-19 Vaccine Breakthrough Infections in Highly Vaccinated Israel – the Effects of Waning Immunity and Third Vaccination Dose

Daihai He, The Hong Kong Polytechnic University, daihai.he@polyu.edu.hk

Abstract

In August 2021, a major wave of the SARS-CoV-2 Delta variant erupted in the highly vaccinated population of Israel. The transmission advantage of the Delta variant enabled it to replace the Alpha variant in approximately two months. The outbreak led to an unexpectedly large proportion of breakthrough infections (BTI) -- a phenomenon that received worldwide attention. The BTI proportion amongst new cases in the age group of 60+ years reached as high as ~85% in August 2021. Most of the Israeli population, especially those aged 60+, received their second dose of the vaccination four months before the invasion of the Delta variant. Hence, either the vaccine induced immunity dropped significantly or the Delta variant possesses immunity escaping abilities, or both. In this work, we analyzed and modeled data obtained from the Israeli Ministry of Health, to help understand the epidemiological factors involved in the outbreak. We propose a mathematical model that captures a multitude of factors, including age structure, the time varying vaccine efficacy, time varying transmission rate, BTIs, reduced susceptibility and infectivity of vaccinated individuals, protection duration of the vaccine induced immunity, and the vaccine distribution. We fitted our model to cases among vaccinated and unvaccinated, for <60 and 60+ age groups, and quantified the transmission rate, the vaccine efficacy over time and the impact of the third dose vaccine. We found that the peak transmission rate of the Delta variant was 1.96 times higher than the Alpha variant. The vaccine efficacy against infection dropped significantly from >90% to ~40% over 6 months, and that the immunity protection duration is consistent with a peaked Gamma distribution. Therefore, given a breakthrough infection, the vaccine efficacy was 73.5% against severe outcome over the aforementioned period. We further performed model simulations and quantified “what if” scenarios examining what would happen if the booster not have been rolled out. We estimated that approximately 3.98 million infections (95%CI 3.02, 4.96) were prevented by vaccination overall, and 1.21 million infections (95%CI 0.79, 1.6) by the booster. The application of this framework can help elucidate important factors concerning epidemic outbreak dynamics and highlight routes of action to mitigate their spread.

Modelling Immunity and Social Distancing

Jane Heffernan, York University, jmheffer@yorku.ca

Abstract

Immunity protects individuals and populations from infection and severe infection outcomes. Social distancing also provides these effects. In this talk I will introduce some mathematical models of infectious diseases that consider immunity and social distancing effects in isolation, and in combination. An application to COVID-19 will be discussed.

The Impact of Toxicants on Population Dynamics in Polluted Aquatic Environments

Qihua Huang, Southwest University, qihua@swu.edu.cn

Abstract

We develop several toxin-mediated population models (including single-species model, competition model, and predator-prey model) to study the effects of toxicants on long-term dynamics of species in aquatic ecosystems. The models incorporate both direct and indirect toxic effects on the species. The direct effects of toxins typically reduce population abundance by increasing mortality and reducing reproduction. However, the indirect effects, which are mediated through interactions between species plus different vulnerabilities of species to toxins, affect long-term outcomes in many counterintuitive ways. It turns out in toxin-dependent competition dynamics, sublethal toxins may boost coexistence of two species (hence keep species diversity in ecosystems) by reducing the abundance of the predominant species; sublethal toxins may overturn and exchange roles of winner and loser in competition; sublethal toxins may also induce different types of bistability of the competition dynamics, where the competition outcome is doomed to exclusion or coexistence, depending on initial population densities. In toxin-dependent food web dynamics, intermediate toxin concentrations may affect predators disproportionately through biomagnification, leading to reduced abundance of predators and increased abundance of the prey; sublethal toxins may also reduce population variability by preventing populations from fluctuating around a coexistence equilibrium; intermediate environmental toxins may induce bistable dynamics, in which different initial population levels produce different long-term outcomes.

A Spatial Transmission Model for Enhancing the Effectiveness of Wolbachia in Controlling the Spread of Mosquito-Borne Diseases

James M. Hyman, Tulane University, mhyman@tulane.edu

Abstract

Wolbachia is a natural bacterium that can infect mosquitoes and reduce their ability to transmit mosquito-borne diseases, such as dengue fever, malaria, Zika, and chikungunya. Field trials and modeling studies have shown that the fraction of infection among the mosquitoes must exceed a threshold level for the infection to persist. To capture this threshold condition, it is critical to consider the spatial heterogeneity in the distributions of the infected and uninfected mosquitoes created by a local release of the infected mosquitoes. We develop and analyze a partial differential equation (PDE) model to study the invasion dynamics of Wolbachia infection among mosquitoes in the field. Our reaction-diffusion-type models account for the complex vertical transmission and the spatial mosquito dispersion. We characterize the threshold for a successful invasion with a bubble-shaped distribution. The critical bubble is optimal in its release size compared to other spatial profiles in a one-dimensional landscape. The fraction of infection near the release center is higher than the threshold level for the corresponding homogeneously mixing ODE models. We show that the proposed spatial models give rise to the traveling waves of Wolbachia infection when above the threshold. We quantify how the threshold condition and traveling-wave velocity depend on the diffusion coefficients and other model parameters. This research was done in collaboration with Zhuolin Qu and Tong Wu at the University of Texas, San Antonio.

A Statistical Block Imputation Method for Single-cellRNA-seq Data

Shuilin Jin, Harbin Institute of Technology, jinsl@hit.edu.cn

Abstract

Single-cell RNA sequencing (scRNA-seq) technologies obtain gene expression at single-cell resolution and provide a tool for exploring cell heterogeneity and cell types. As the low amount of extracted mRNA copies per cell, scRNA-seq data exhibit a large number of dropouts, which hinders the downstream analysis of the scRNA-seq data. We propose a statistical method, SDImpute (Single-cell RNA-seq Dropout Imputation), to implement block imputation for dropout events in scRNA-seq data. SDImpute automatically identifies the dropout events based on the gene expression levels and the variations of gene expression across similar cells and similar genes, and it implements block imputation for dropouts by utilizing gene expression unaffected by dropouts from similar cells. The results of experiments suggest that SDImpute is an effective tool to recover the data and preserve the heterogeneity of gene expression across cells and improves the accuracy of the downstream analysis including clustering, visualization, and differential expression analysis.

Epidemic Threshold and Ergodicity of an SIS Model in Switched Networks

Zhen Jin, Shanxi University, jinzhn@263.net

Abstract

Because of individuals' random walk, people have different behaviors and thus have different social contact patterns. Therefore, topology of human social contact networks is time-varying. In this talk, we investigate dynamic characteristics of an SIS network epidemic model with Markovian switching. An epidemic threshold is established for the extinction and permanence of the model, which is related to the steady-state distribution of the Markov chain. An interesting result is that when the epidemic is permanent in one network but extinct in another, under network switching mechanisms, it may be either permanent or extinct depending on the steady-state distribution of the Markov chain. This reveals the important role of the Markov chain in epidemic evolution. This work shows that the epidemic propagation in switched networks is quite different from that of static networks. In addition, based on Lyapunov function method, positive recurrence and ergodicity of stochastic spreading processes are also discussed. Finally, numerical simulations are carried out to illustrate our theoretical results.

异质性干细胞增殖过程的熵变化

Jinzhi Lei, Tiangong University, jzlei@tiangong.edu.cn

Abstract

干细胞在多细胞生物体内广泛存在, 其增殖过程在生命体的生长、发育、衰老、组织修复过程中起着重要作用. 正常组织中的细胞增殖过程受到严格的控制, 干细胞的异常增殖与恶性肿瘤、肥胖症、再生障碍性贫血等疾病有密切关系. 生命体内异质性细胞的增殖过程是复杂的动力系统行为, 干细胞异常增殖过程伴随细胞的可塑性变化和细胞间相互作用的再平衡过程, 如何对这一过程进行定量描述是重要的研究课题. 本文构建包含细胞的增殖分化指标和异常增殖性指标异质性的干细胞增殖模型, 通过所建立的模型研究由于微环境变化引起的细胞异常增殖过程的熵变化, 建立不同增殖条件下的系统熵变化与宏观动力学和系统参数之间的关系. 结果表明, 在细胞微环境变化引起异常增殖和恢复的过程中, 系统的熵与细胞数量之间存在对应关系, 而与微环境变化的路径无关. 此外, 熵对细胞数量的依赖关系在异常增殖和恢复阶段表现出不同的行为, 显示了生物过程的微观不可逆性. 本文从物理学的角度对细胞异常增殖过程中熵变化与细胞数量变化的动力学给出定量刻画, 为定量描述异质性干细胞增殖过程给出新的研究思路.

Discrete Models of Interactive Wild and Sterile Mosquitoes

Jia Li, The University of Alabama in Huntsville and Guangzhou University, li@math.uah.edu

Abstract

To study the dynamics of interactive wild and sterile mosquitoes and their impacts on the transmissions of mosquito-borne diseases, mathematical models have been formulated and investigated. In this talk, we present several discrete-time models based on systems of difference equations. The survival functions are assumed to be of either Ricker-type or Beverton-Holt-type nonlinearity. We particularly introduce homogeneous and stage-structured models with time steps in more general settings such that survivals are included at each time step. We assume that sterile mosquitoes are released and their number in the field is kept at a constant level. We study the interactive dynamics of wild and sterile mosquitoes where only sexually active sterile mosquitoes are considered. We determine threshold values of releases and investigate the model dynamics for both homogeneous and stage-structured populations. We also discuss the models where sterile mosquitoes are released periodically and impulsively. This talk is based on the joint work with Professor Jianshe Yu.

Modeling and Research on an Immuno-Epidemiological Coupled System with Coinfection

Xuezhi Li, Henan Normal University, xzli66@126.com

Abstract

In this talk, a two-strain model with coinfection that links immunological and epidemiological dynamics across scales is formulated. On the with-in host scale, the two strains eliminate each other with the strain having the larger immunological reproduction number persisting. However, on the population scale coinfection is a common occurrence. Individuals infected with strain one can become coinfected with strain two, and similarly for individuals originally infected with strain two. The immunological reproduction numbers Rj , the epidemiological reproduction numbers Rj and invasion reproduction numbers Rij are computed. Besides the disease-free equilibrium, there are strain one and strain two dominance equilibria. The disease-free equilibrium is locally asymptotically stable when the epidemiological reproduction numbers Rj are smaller than one. In addition, each strain dominance equilibrium is locally asymptotically stable if the corresponding epidemiological reproduction number is larger than one and the invasion reproduction number of the other strain is smaller than one. The coexistence equilibrium exists when all the reproduction numbers are greater than one. Simulations suggest that when both invasion reproduction numbers are smaller than one bistability occurs with one of the strains persisting or the other, depending on initial conditions.

The impulsive harvesting and evolving of domain in diffusive models

Zhigui Lin, Yangzhou University, zglin68@hotmail.com

Abstract

In order to understand how the combination of domain evolution and impulsive harvesting affect the dynamics of a population, we propose a diffusive logistic population model with impulsive harvesting on a periodically evolving domain. Initially the ecological reproduction index of the impulsive problem is introduced and given by an explicit formula, which depends on the domain evolution rate and the impulsive function. Then the threshold dynamics of the population under monotone or nonmonotone impulsive harvesting is established based on this index. Finally numerical simulations are carried out to illustrate our theoretical results, and reveal that a large domain evolution rate can improve the population survival, no matter which impulsive harvesting takes place. On the contrary, impulsive harvesting has a negative effect on the population survival, and can even lead to the extinction of the population.

An Age-Structured Mathematical Model on Mumps Outbreaks in Jiangsu Province

Xianning Liu, Southeast University, liuxn@swu.edu.cn

Abstract

Measles, mumps and rubella (MMR) vaccine program was introduced in Jiangsu province of China in May 2008 and has been greatly contributed to decreasing of mumps cases. However, mumps has been resurging since May 2015. A number of studies have put forward that the resurgence of mumps is due to vaccine failure. We investigated the other reasons for the resurging of mumps, such as the changes in seasonal transmission patterns and demographic structures, by using an age-structured mathematical model. We divided the history (January 2005 to May 2019) of mumps epidemics of Jiangsu province into three different stages: No vaccine stage (January 2005 to December 2008), effectively controlled stage (January 2009 to December 2014) and resurgence stage (January 2015 to May 2019). The features of mumps epidemics in three stages are compared under different demographic structures with same physical contact rate. The mumps transmission rate was increased in summer and dropped in November in stage III compared with that in stage I. The changes in demographic structures give a good explanation why the mumps outbreaked among children around 10 years old in stage I and around 5 years old in stage III. We have a conclusion that the vaccine failure, changes in seasonality and demographic structures were associated with the mumps outbreaks in recent years in Jiangsu province, China. We give the patterns of mumps dynamics considering age, vaccine, seasonality and demographic structures, which can help health program planners to implement more preventive interventions in mumps control during the period of higher risk of infection.

基于贝叶斯进化分析的HIV耐药传播动力学研究

Jie Lou, Shanghai University, jie.lou@126.com

Abstract

首先，针对中国异性间HIV/AIDS传播的四个主要亚型(CRF01AE, CRF07BC, CRF08BC和CRFBC)共计912条基因序列数据, 我们应用贝叶斯系统发育分析分别推断它们各自的最近源祖先时间和有效再生数, 以追溯HIV/AIDS在该人群中的传播动力学历史. 其次, 基于HIV/AIDS在异性间的传播特征, 我们建立了动力学模型来预测HIV耐药株在未来的传播趋势. 然后，通过马尔可夫蒙特卡洛(MCMC)方法, 我们把系统发育分析推断出的再生数与动力学模型推导出的再生数进行拟合, 得到了动力学模型中的不确定参数. 最后，考虑不同的HIV/AIDS防控措施对动力学模型进行数值模拟, 我们预测和对比了不同措施对耐药株传播的影响.

Coexistence of Strains in Some Reaction-Diffusion Systems

Yuan Lou, Shanghai Jiao Tong University, lou@math.ohio-state.edu

Abstract

We study the global dynamics of some reaction-diffusion systems for multiple strains and  investigate how the coexistence of strains is impacted by the movement of populations and spatial heterogeneity of the environment. For the case of two strains, general conditions for the existence, uniqueness and stability of coexistence steady states are found. Surprisingly, when there is no coexistence of strains, it is possible for the ``weak" strain to be dominant for intermediate diffusion rates, in strong contrast to small and large diffusion cases where the ``weak" strain goes extinct.  This talk is based on joint work with RachidiSalako.

A Quantification of Long Transient Dynamics

Felicia Magpantay, Queen’s University, felicia.magpantay@queensu.ca

Abstract

The stability of equilibria and asymptotic behaviors of trajectories are often the primary focuses of mathematical modeling. However, many interesting phenomena that we would like to model, such as the “honeymoon period” of a disease after the onset of mass vaccination programs, are transient dynamics. Honeymoon periods can last for decades and can be important public health considerations. In many fields of science, especially in ecology, there is growing interest in a systematic study of transient dynamics. In this work, we attempt to provide a technical definition of “long transient dynamics” such as the honeymoon period and explain how these behaviors arise in systems of ordinary differential equations. We define a transient center, a point in state space that causes long transient behaviors, and derive some of its properties. In the end, we define reachable transient centers, which are transient centers that can be reached from initializations that do not need to be near the transient center.

The Impact of a Single Individual on the Spread of an Epidemic

Joel Miller, La Trobe University, joel.c.miller.research@gmail.com

Abstract

Many of the policy responses to the COVID-19 pandemic have involved restricting people’s behavior. Often these have been associated with penalties to induce compliance. When designing a policy, ethical considerations suggest that the penalties for an action should be proportional to the harm caused by that action. In this talk, I will explore the expected impact on the final size of an epidemic of a single individual changing behavior as well as the combined impact of a group. Due to the convexity of the final size relation, the marginal benefit of an individual changing behavior to prevent transmission is increased if others are also taking actions to prevent transmission. This benefit is largest when the reproduction number is close to 1.This talk will also have an introduction to the use of Probability Generating Functions in modeling infectious disease transmission.

MD Simulation of Biomolecules and its Complexes, and Parallel Numerical Integration of Large Systems of Differential Equations

Evgeni Nurminski, Far Eastern Federal University, nurminskiy.ea@dvfu.ru

Abstract

This talk describes the initial thermal denaturation of the monomer and trimer of a bacterial porin and the dimer of the enzyme alpha-galactosidase from a marine bacterium. 3D-structures were built and MD simulations were carried out of the polyelectrolyte complex of chitosan and kappa-caraginan and fucoidan and chitosan nanoparticles at different ratios of molecules in the complex. This simulation is intended to be used as a test case for an new MD-simulator based on Parker-Sochacki ODE solver which produces continuous-time representation of the system trajectory and allows for parallel implementation. The basics of this approach and implementation challenges are described.

Recruitment Dynamics of Social Insect Colonies

Zhipeng Qiu, Nanjing University of Science and Technology, nustqzp@njust.edu.cn

Abstract

Recruitment plays a vital role in the ecological and evolutionary successes of social insect colonies. In this paper, we formulate a four-compartment model and its simplified version to explore how we should model the recruitment dynamics of workers in social insect colonies properly. Our four-compartment model has the components of the unalarmed patrollers, the alarmed patrollers, the alarmed recruiters, and the available workers, while its simplified version has three components where we combine the unalarmed patrollers and the alarmed patrollers into the patrollers. We perform complete mathematical and bifurcation analyses on both the full system and its simplified system. We have many interesting findings, including that (i) the simplified three-compartment system has only simple equilibrium dynamics, i.e., no periodic and chaotic dynamics; (ii) the four compartment system has very complex dynamics; for example, it can have up to three subcritical Hopf bifurcations, two supercritical Hopf bifurcations, two limit point bifurcations, and a fold bifurcation of the limit cycle. Those important results provide theoretical guidance for modeling and studying recruitment dynamics of social insect colonies: It is critical to have proper compartments for biological systems as the number of compartments could lead to totally different dynamics, and hence affect policy-making. This is a joint work with Tao Feng and Yun Kang.

Prediction of Readmission and Survival Analysis of Elderly Patients with Heart Failure Based on Machine Learning

Jingli Ren, Zhengzhou University, renjl@zzu.edu.cn

Abstract

Using machine learning, we establish an objective and accurate prediction model for the readmission of patients with heart failure and a survival analysis model for patients with heart failure. The former uses the clinical data of patients to predict their readmission, and then determine early intervention to effectively avoid the high mortality caused by emergency admission; The latter is to evaluate the survival probability of patients with heart failure and analyze the impact of clinical symptoms on patients, and assist doctors to treat patients at different stages of development, so as to reduce the risk of death.

Spatial Propagation in a Within-Host Viral Infection Model

Shigui Ruan, University of Miami, shiguiruan@yahoo.ca

Abstract

Recent experimental evidence suggests that spatial heterogeneity plays an important role in within-host infections caused by different viruses including hepatitis B virus (HBV), hepatitis C virus (HCV), and human immunodeficiency virus (HIV). In order to examine the spatial effects of viral infections, we study the asymptotic spreading in a within-host viral infection model which describes the spatial expansion speeds of viruses and infected cells within an infected host. We first establish the boundedness of solutions to the Cauchy problem via local Lp-estimates and dual arguments. Then the spreading speed is estimated when the basic reproduction number of the corresponding kinetic system is larger than one. More precisely, the upper bounds of the spreading speed are given by constructing suitable upper solutions while the lower bounds of the spreading speed are obtained by introducing an auxiliary equation with nonlocal delay. When the basic reproduction number of the corresponding kinetic system is less than one, the virus dies out uniformly. Finally, we present some numerical simulations to illustrate our theoretical findings and discuss the biological relevance of these results. (Based on a joint paper with Xin-Jian Wang and Guo Lin, Stud. Appl. Math. 2022)

A multilayer Temporal Network Model for STD

Caterina Scoglio, Kansas State University, caterina@ksu.edu

Abstract

Sexually transmitted diseases (STD) modeling has used contact networks to study the spreading of pathogens. Recent findings have stressed the increasing role of casual partners, often enabled by online dating applications. We study the Susceptible-Infected-Susceptible (SIS) epidemic model –appropriate for STDs– over a two-layer network aimed to account for the effect of casual partners in the spreading of STDs. In this novel model, individuals have a set of steady partnerships (links in layer 1). At certain rates, every individual can switch between active and inactive states and, while active, it can establish casual partnerships with some probability with active neighbors in layer 2 (whose links can be thought as potential casual partnerships). Individuals that are not engaged in casual partnerships are classified as inactive, and the transitions between active and inactive states are independent of their infectious state. We use mean-field equations as well as stochastic simulations to derive the epidemic threshold, which decreases substantially with the addition of the second layer. Interestingly, for a given expected number of casual partnerships, which depends on the probabilities of being active, this threshold turns out to depend on the duration of casual partnerships: the longer they are, the lower the threshold.

Optimization Models for Improving Access for Target Populations during Pandemics

Bismark Singh, Friedrich-Alexander-Universität Erlangen-Nürnberg, bismark.singh@fau.de

Abstract

Estimating access for critical resources during an epidemic outbreak is of vital importance for public policy and healthcare planning. Access informs the extent to which a target population is safely covered.  As an example, rapid diagnostic testing for COVID-19 has remained a key to guiding social distancing orders and containing emerging disease clusters by contact tracing and isolation. However, particularly in the US, not all communities have had adequate access for tests. Next, as new antivirals – such as Paxlovid - become available for the current COVID-19 pandemic, the question of choosing sites for provisioning these drugs is again of importance. We present a collection of optimization models that we have developed over the past several years, and applied both to the 2009 H1N1 (retrospectively) and current COVID-19 (dynamically) pandemics.

Spatiotemporal Dynamics of a Diffusive Consumer-Resource Model with Explicit Spatial Memory

Yongli Song, Hangzhou Normal University, songyl@hznu.edu.cn

Abstract

Spatial memory is inevitable in animal movement modeling but elusive in many classical models. A nonlocal integral term involving space is a traditional way to incorporate spatial memory, but the actual spatial memory should depend on past information so that delay naturally arises. We propose a new consumer-resource model with random and memory-based diffusions in which the resource species has nomemory or cognition, whereas the consumer species has spatial memory. By using the memory-based diffusion coefficient and the averaged memory period of the consumer as the control parameters, we find Hopf bifurcations and stability switches occur and spatially nonhomogeneous periodic solutions are generated. It is well known that prey-taxis enhances the stability of a homogeneous coexistence state in a predator–prey system, and here we show that memory-based prey-taxis can destabilize a constant coexistence and generate complex spatiotemporal pattern formation.

干旱半干旱区域植被斑图动力学研究

Guiquan Sun, North University of China, gquansun@126.com

Abstract

近几十年来，在全球变暖和人类活动因素的共同影响下，干旱半干旱区域的植被退化以及荒漠化现象越来越严重，这些现象已经对人类生存和生态环境可持续发展构成了严重威胁。为此，我们细致分析了参数的细微变化如何影响植被斑图的结构，并研究了气候变化对植被斑图演化的影响。

新冠疫情时空疫情数据与随机模型分析

SanyiTang,Shaanxi Normal University, sytang@snnu.edu.cn

Abstract

随着新冠病毒的不断变异，其传播快、隐匿性强的特点给中国的防控带来了新的挑战。为了应对这一挑战，社区防控区域按照封控区、管控区、防范区科学划定，但如何量化并构建传播动力学模型，分析划分防控区域对大中城市的疫情时空分布、遏制疫情扩散和蔓延的影响等具有重要的意义。利用石家庄、南京、西安市等地疫情数据进行时空统计分析，根据病例的地理位置分布，划分为不同的斑块，考虑随机性、斑块间病例的流动及防控区域划分，建立离散随机传播动力学模型，研究提前封锁、管控强度和时机等对疫情的影响，为基于时空的精准疫情防控策略提供决策依据。

Stochastic Modeling and Analysis in Mathematical Biology

Wendi Wang, Southwest University, wendi@swu.edu.cn

Abstract

First, I introduce the basic approaches of stochastic modeling in biology. Then I present our studies for the dynamical behaviors of the competition. Models and the mixed mode of competition with predation. After that, I show our studies on modeling of prostate cancers. We aim to find out the influences of stochastic noises on the persistence and extinction of the populations.

Global Dynamics and Spatiotemporal Heterogeneity of Predator-Prey Systems with Acceleration

Zhian Wang, The Hong Kong Polytechnic University, zhi.an.wang@polyu.edu.hk

Abstract

Conventional prey-taxis systems assume that prey-tactic velocity is proportional to the prey density gradient. However many experiments exploring the predator-prey interactions show it is the predator's acceleration instead of velocity that is proportional to the prey density gradient in the prey-tactic movement, which we call non-conventional prey-taxis. In this talk, we shall discuss the qualitative behavior of such non-conventional prey-taxis systems including global existence and stability of solutions. We also use numerical simulations to demonstrate that spatially inhomogeneous time-periodic patterns will typically arise from the non-conventional prey-taxis system. Noticing that conventional prey-taxis systems are unable to produce spatial patterns, our results imply that the non-conventional prey-taxis is indeed more appropriate than conventional prey-taxis to interpret the spatial heterogeneity resulting from the predator-prey interactions.

The Multi-Scale Dynamic Models with Application to the COVID-19 Pandemic

Yanni Xiao, Xi’an Jiaotong University, yxiao@mail.xjtu.edu.cn

Abstract

The COVID-19 pandemic has caused worrying concern amongst the public and health authorities since early 2020. Modeling of this novel coronavirus also presents us a great challenge. In this talk I initially summarize what we have done on the prediction of COVID-19 pandemic and effect of massive movement on the possible outbreak. I then present our recent work on COVID-19 infection, including a multi-scale models describing the multiple outbreaks and a stochastic individual based model on complex networks with four layers. We would like to investigate how behavior changes, vaccination and relaxation of non-NPIs affect the development of COVID-19 infections. Finally I shall give some considerations and thoughts on modelling COVID-19 infections and concluding remarks.

Wolbachia Spread Dynamics in Stochastic Environments

Jianshe Yu, Guangzhou University, jsyu@gzhu.edu.cn

Abstract

A novel strategy for mosquito-borne disease control is to use the bacterium Wolbachia to block virus transmission. It requires releasing Wolbachia-infected mosquitoes to exceed a threshold level. Since an accurate forecast for temperature and rainfall, the major environmental conditions regulating the mosquito dynamics, is often not available over a long time period, it is important to explore how the threshold releasing level changes in random environments. By comparing the dynamics between the stochastic system and constructed auxiliary systems, combined with other techniques, we provide sharp estimates on the threshold releasing level for Wolbachia fixation. In addition, we prove that the threshold level is, surprisingly, defined by a deterministic curve that does not fluctuate with environmental conditions.

Stochastic Switches of Eutrophication and Oligotrophication: Modeling Extreme Weather via Non-Gaussian Lévy Noise

Sanling Yuan, University of Shanghai for Science and Technology, sanling@usst.edu.cn

Abstract

Disturbances related to extreme weather events, such as hurricanes, heavy precipitation events, and droughts, are important drivers of evolution processes of a shallow lake ecosystem. A non-Gaussian 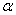-stable Lévy process is esteemed to be the most suitable model to describe such extreme events. This paper incorporates extreme weather via 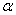-stable Lévy noise into a parameterized lake model for phosphorus dynamics. We obtain the stationary probability density function of phosphorus concentration and examine the pivotal roles of 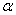-stable Lévy noise on phosphorus dynamics. The switches between the oligotrophic state and the eutrophic state can be induced by the noise intensity 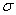, skewness parameter , or stability index 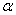. We calculate the mean first passage time, also referred to as the mean switching time, from the oligotrophic state to the eutrophic state. We observe that the increased noise intensity, skewness parameter, or stability index makes the mean switching time shorter and thus accelerates the switching process and facilitates lake eutrophication. When the frequency of extreme weather events exceeds a critical value, the intensity of extreme events becomes the most key factor for promoting lake eutrophication. As an application, we analyze the available data of Lake Taihu (2014–2018) for monthly precipitation, phosphorus, and chlorophyll-a concentrations and quantify the linkage among them using the Lévy-stable distribution. This study provides a fundamental framework to uncover the impact of any extreme climate event on aquatic nutrient status.

Finite-Time Stability and Optimal Impulsive Control for Age-Structured HIV Model with Time-Varying Delay and Levy Noise

Qimin Zhang, Ningxia University, zhangqimin64@sina.com

Abstract

In this talk，we investigate the finite-time stability and optimal impulsive control for stochastic age-structured HIV model with time-varying delay. A stochastic noise is introduced by the Levy process to describe phenomena that a continuous stochastic process (e.g., white noise) cannot describe. By employing the comparison theorem and the bounded impulsive interval method, we obtain the sufficient conditions of finite-time stability for a stochastic HIV system. The effects of impulse, delay and Levy noise on the finite-time stability are considered in our sufficient conditions. Furthermore, optimal impulsive control is studied to seek the optimal and cost-effective strategy for HIV treatments, which shows that control strategies play an important role in HIV virus transmissions.

Bifurcations in a Discrete Predator-Prey Model

Weinian Zhang, Sichuan University, matzwn@163.com

Abstract

Recently a discrete-time prey-predator model with Holling type II was discussed for its bifurcations so as to show its complicated dynamical properties. Simulation illustrated the occurrence of invariant cycles. In this talk we first clarify the parametric conditions of non-hyperbolicity, correcting a known result. Then we apply the center manifold reduction and the method of normal forms to completely discuss bifurcations of codimension 1. We give bifurcation curves analytically for transcritical bifurcation, flip bifurcation and Neimark-Sacker bifurcation separately, showing bifurcation phenomena not indicated in the previous work for the system.

Analysis of a Two-Strain Malaria Transmission Model with Spatial Heterogeneity and Vector-Bias

Hongyong Zhao, Nanjing University of Aeronautics and Astronautics, hyzho1967@126.com

Abstract

In this talk, I will introduce a reaction-diffusion malaria model which incorporates vector-bias, spatial heterogeneity, sensitive and resistant strains. The main question that I study is the threshold dynamics of the model, in particular, whether the existence of spatial structure would allow two strains to coexist. Numerical simulations reinforce these analytical results and demonstrate epidemiological interaction between two strains, discuss the influence of resistant strains and study the effects of vector-bias on the transmission of malaria.

Spatial Dynamics of Species with Annually Synchronized Emergence of Adults

Xiaoqiang Zhao, Memorial University of Newfoundland, zhao@mun.ca

Abstract

In this talk, I will report our recent research on the spatial dynamics of species growth with annually synchronous emergence of adults by formulating an impulsive reaction-diffusion model. With the aid of the discrete-time semiflow generated by the one-year solution map, we establish the existence of the spreading speed and traveling waves for the model on an unbounded spatial domain. It turns out that the spreading speed coincides with the minimal speed of traveling waves, regardless of the monotonicity of the birth rate function. We also investigate the model on a bounded domain with a lethal exterior to determine the critical domain size to reserve species persistence. Numerical simulations are illustrated to confirm the analytical results and to explore the effects of the emergence maturation delay on the spatial dynamics of the population distribution. In particular, the relationship between the spreading speed and the emergence maturation delay is found to be counterintuitively variable.

Modelling and Risk Assessment of the Emerging Monkeypox Transmission in Canada

Huaiping Zhu, York University, huaiping@yorku.ca

Abstract

        Monkeypox is a viral zoonosis which was first identified in 1958 in a laboratory monkey.  It has been nearly one month since the first confirmed case of monkeypox in the United Kingdom on May 6, 2022, it has spread with increasing cases to non-African countries including Canada as an emerging infection. In this talk, I will present a modelling study to assess the risk of monkeypox in Canada. Using one health approach, we establish a dynamical model to mimic the spreading of the virus in humans, rodents, and non-human primates (like monkeys) and distinguish the human population into higher and low-risk groups. While the animal reservoir is the key element in the modelling of zoonosis disease, we will emphasize the role and transmission of the virus in high-risk group of man to man sexual connected humans.  Using the modelling, I will present our preliminary results on the risk assessment of the virus in Canada, I will also discuss to identify public health measures that need to be enforced to contain the spread to prevent any potential emerging outbreak. We also investigate the animal monkeypox infections will exarate the monkeypox transmission risk among the population and discuss the importance of surveillance of animal infection of monkeypox to predict the possible monkeypox outbreak. This is a joint work with Pei Yuan, Yi Tan, Liu Yang, and Nick Ogden.

A New Perspective on Infection Forces with Demonstration by a DDE Infectious Disease Model

Xingfu Zou, University of Western Ontario, xf2zou@gmail.com

Abstract

In this talk, we will revisit the notion of infection force from a new angle which can offer a new perspective to motivate and justify some infection force functions. Our approach not only can explain many existing infection force functions in the literature, it can also motivate new forms of infection force functions, particularly infection forces depending on disease surveillance of the past. As a demonstration, we propose an SIRS model with delay. We comprehensively investigate the disease dynamics represented by this model, particularly focusing on the local bifurcation caused by the delay and another parameter that reflects the weight  of the past epidemics in the infection force. We confirm Hopf bifurcations both theoretically and numerically. The results show that depending on how recent the disease surveillance data are, their assigned weight may have a different impact on disease control measures.

Mathematical Model-Based Adaptive Therapy for Cancer

Xiufen Zou, Wuhan University, xfzou@whu.edu.cn

Abstract

Adaptive therapy, a new therapeutic strategy, is increasingly applied in the treatment of cancer. It is a great challenge to identify the therapeutic period and dose in adaptive therapy. In this study, we establish a competitive model between drug-sensitive and drug-resistant cancer cells. Theoretical analysis, including the stability of equilibrium points and the existence of periodic solutions, validates the interpretability of the model. The available data for prostate cancers are used to identify the model parameters. Furthermore, we propose a new dynamic optimization problem with constraints to establish the adaptive therapeutic schedule for prostate cancer, and an optimal set of decisions in this optimization problem represents the therapeutic period and dose in adaptive therapy. Through numerical simulations and quantitative analysis, we compare our therapeutic schedule and current adaptive therapeutic schedules in patients with prostate cancer in three aspects: the total drug dose, the peak number of drug-resistant cancer cells and the survival time. These results demonstrate that our therapeutic framework is superior to the current adaptive therapeutic schedules. The proposed therapeutic framework could provide an identifiable adaptive therapy to achieve personal and precise treatment for prostate cancer.